概要

　ある一定の領域に存在する生物およびそれらを取り巻く非生物的環境をまとめて一つの系と見なした生態系を数学的に扱う生態系の数理モデル、その中でも特に感染症の数理モデルを、主要な研究テーマとしています。
　感染症の数理モデルには、考えている人口集団を感染状態によっていくつかの状態に分ける「コンパートメントモデル」と呼ばれるものがあり、それぞれの状態の時間変化は微分方程式あるいは差分方程式によって記述されます。最も基本的なモデルは、全人口を未感染人口S、 感染人口I、 回復人口Rの三つのグループに分けたSIRモデルであり、このモデルに基づいて例えば最終的に全人口のうちのどこまで感染が広がり、どのくらいの時間で終息するかといった解析を行う事が可能です。これらのモデルは「力学系」として一般的な議論を行う事ができますが、一方でそれぞれの感染症特有の性質により、興味深い性質を示す場合もあります。純粋数学的な安定性等の議論以外にも、現実の感染症において観測される現象を比較的単純なモデルで説明できるかが重要です。

応用例

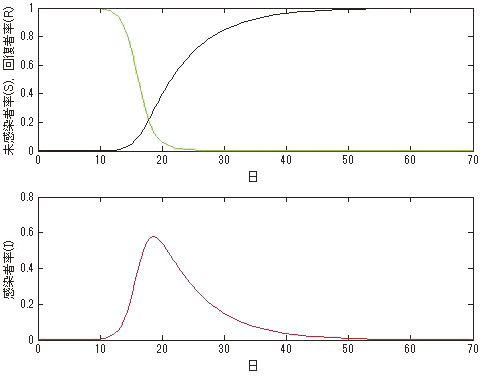
より現実の感染症に即した解析を行うためには、例えば感染してから実際に発症するまでの時間差を考慮するといった様々な効果をモデルに取り入れる必要がありますが、一方でいたずらにモデルを複雑化すれば、単に解析が難しくなるだけではなく、「説明のための説明」になりがちです。最小限の効果を取り込んだ単純なモデルで、十分に多くの現象を説明できることが重要であり、そのようなモデルの開発と解析が今後の発展方向となるでしょう。
感染症の数理モデルの解析を進める事によって、例えばインフルエンザで見られるような世界的流行がどのようにして起こり、またどのような対策を行えば防げるのかを見出す事も将来的には可能となるでしょう。

研究設備

理論・数値計算に基づき、生態学モデルに関する解析を行っています。
数学分野の場合、特に大型の研究設備といったものは存在しない場合が多く、その代わりに理工系の他分野より多く研究室に蔵書している専門書が、研究設備といえるでしょう。また、壁一面の大型黒板は不可欠な「実験道具」です。

共同研究・外部機関との連携への期待

重要な感染症の流行の予測、拡大防止を可能とするための、研究機関等との研究開発